Las gráficas del seno y del coseno son iguales, aunque desfasadas 90º. Lo que equivale a decir que cos α = sen(π/2+α), con los ángulos en radianes, donde π/2 = 90º. Foto de Lombard Street, San Francisco, tomada en larga exposición por Sean Arbabi-
No hay película de piratas que se precie en que no salga un sextante, el precioso aparato para medir ángulos y establecer la posición del barco. Se compone de anteojo, espejos y un arco graduado y se pueden comprar imitaciones de los antiguos. Foto Timitrius, en el Museo de Historia de la Ciencia.
Dicen que la salud se tiene con los pies calientes y la cabeza fría, aunque los matemáticos se calientan la cabeza buscando nuevas funciones y con las trigonométricas resolvieron la ecuación del calor con series de Fourier. Y para un cálido hogar están los preciosos edredones matemáticos de Elaine Krajenke Ellison, como éste que representa las funciones trigonométricas seno, coseno y tangente rodeados de azulejos geométricos.
El plano cartesiano y circunferencia goniométrica tienen 4 cuadrantes. Y los ángulos mayores de 90º pueden “reducirse” al 1º cuadrante porque los segmentos de su seno (y coseno) son de la misma longitud. Esto se analiza con fórmulas, pero es mucho más práctico visualizarlo en un esquema. Foto Tanha.
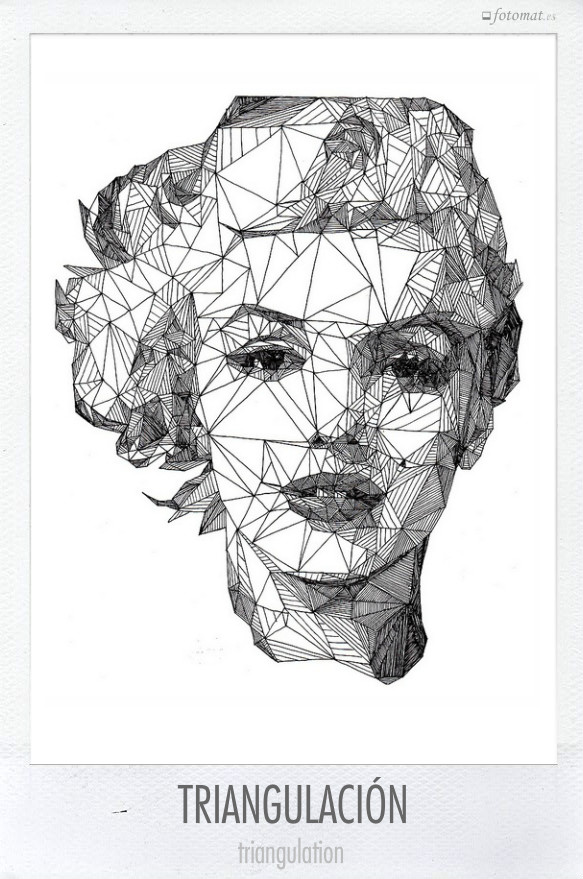
La realidad es compleja y en nuestras limitaciones, buscamos la línea recta para comprender, diseñar y construir, salvo que seamos Gaudí. Y para acercarse a la imagen real se utilizan triangulaciones en arte, diseño, ingeniería, GPS o renderización. Foto de un retrato dibujado a mano por Josh Bryan
.jpg "Gráficas de esta función")
Cuando uno se acerca a dividir por cero las cosas se complican. Hay que buscar el límite en el cero. La gráfica ayuda, pero no es definitiva. La curva oscila infinitas veces entre -1 y 1. El Dr. Conroys lo ilustra muy bien, usando el Teorema del Sandwich. Foto del puente de Meydan en Dubai por Elia Locardi, el futuro es ahora.
Las matemáticas llevan el sello del Teorema de Pitágoras. No hay triángulo rectángulo que se le resista. Foto: Sello emitido en Grecia el 20 de agosto de 1955, 2500 años después de la Escuela Pitagórica
Siempre rectos, con sus catetos, su hipotenusa y su teorema de Pitágoras, los triángulos rectángulos son una de las formas más simples para multitud de construcciones y aplicaciones y son la base de la trigonometría. Foto David Keochkerian
Dando una vuelta a tu alrededor recorres 360º sexagesimales. Que serán 400g, si mides en grados centesimales. Ya desde 1843 se empezó a hacer fotografía panorámica en modo plano y actualmente se ofrecen espectaculares vistas navegables como esta de Paris o las que recoge @aomatos en su Blog de Antonio Matos. Y en vivo y en directo carreteras, calles y edificios en Google Street View.
90º<ω<180º. Con esta inclinación la pendiente es negativa. Foto de un diseño decorativo de Yaniss R. Letechipia
.jpg&description=Fotomat y=xsen(1/x) de @notemates "Pin It")
