
Por cada recta del plano hay infinitas rectas paralelas, todas con la misma dirección. Así que podríamos dividir el plano en infinitas direcciones con infinitas rectas cada una. Cosa que se puede hacer también en el espacio 3D. Foto de viñedos por Frank Dietrich.
Archivo de la etiqueta: rectas

Relajante y fresca geometría. Foto Antonio Fidalgo situada en Aveiro, Portugal.

Si una recta es perpendicular a otra, es perpendicular a todas sus paralelas. Y viceversa, si un tubo es perpendicular a la goma de la ducha, todos los tubos paralelos también lo son. Se ve evidente, pero en matemáticas las cosas hay que demostrarlas, apoyarse sólo en la intuición te puede llevar a una ducha de agua fría. Foto Grace Bonney.
Esta entrada va en paralelo a la edición 5.1 del Carnaval de Matemáticas coordinado en titoeliatrondixit
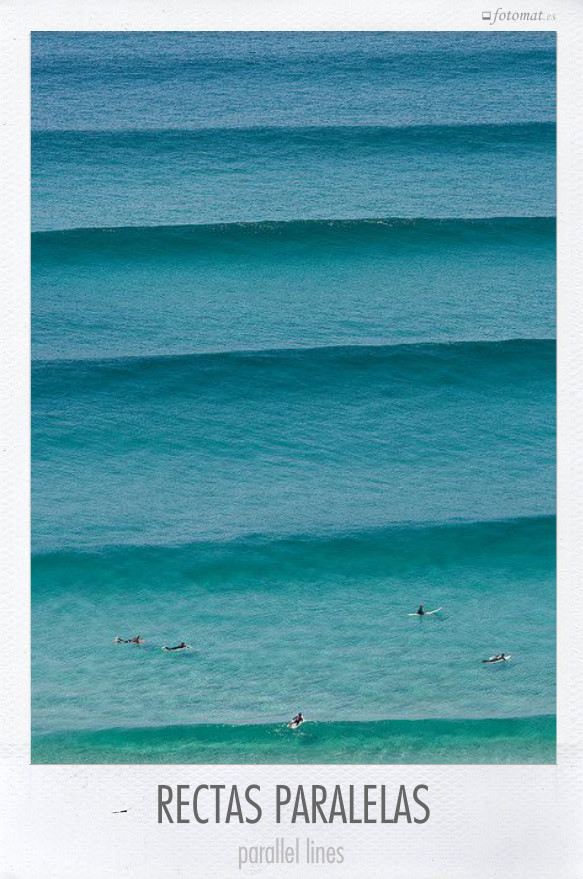
Como los planos paralelos de ayer, tampoco son rectas perfectas, pero la hermosa foto publicada por Hein sugiere un haz de rectas paralelas en el plano infinito del mar.

Un viejo chiste ponía a dos paralelas abrazándose con el pie paralelas aprovechando un descuido de Euclides. Se mantuvo firma Euclides durante siglos, hasta que nuevas geometrías, nuevas teorías, nuevos conceptos encontraron nuevas paralelas. Sin que deje de tener razón Euclides, cada cosa en su sitio. Sobre una preciosa foto de Phillip Alex.

Después de construir la circunferencia y el triángulo no podíamos dejar de ver una perpendicular. Porque la geometría se piensa y representa, pero también se construye con las manos.
Foto Martin Zeinelov.
Esta entrada participa en la edición 4.12310562 del Carnaval de Matemáticas alojado en ::ztfnews.

Por un punto exterior a una recta puede trazarse una paralela, en la geometría euclídea, y también una perpendicular y sólo una. Puede hacerse de manera sencilla con regla y compás. Y también con ecuaciones en geometría analítica, sabiendo que el vector perpendicular a (a,b) es (–b,a). Y también con pájaros, como en la foto de Balan Vinod.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Una línea recta y una parábola se cortan en dos puntos. O en uno o en ninguno. Y, por estas maravillas de las matemáticas, esos puntos se pueden encontrar gráficamente o con unas sencillas ecuaciones. Que tendrán dos soluciones. O una, y decimos que son dos iguales o una doble. O ninguna, y podemos decir que se cortan en puntos imaginarios.
Foto Wayne Simms del puente de Calatrava en Dallas.

Ευκλείδης, Eukleides, Euclides puso las bases de una nueva Geometría con el libro de los Elementos, del que destacó históricamente el 5º postulado. Durante siglos todos los matemáticos han seguido sus pasos. Foto mathieu.

El vector director o direccional de una recta indica su dirección. La cosa tiene sentido y es muy útil para situarla y hallar su ecuación. Foto Kevin Shafer.


