
El concepto de velocidad media es sencillo, basta dividir lo que andas entre lo que tardas, pero para afinar más y trabajar con velocidad instantánea hubo que inventar las derivadas y todo el cálculo infinitesimal de Newton y Leibnitz, con sus épsilons, infinitésimos, límites y funciones continuas, basado todo en los números reales, indispensables para ello. Foto National Geographic.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.
Archivo de la etiqueta: funciones

Una impresionante recta vertical a la que una curva se acerca, se acerca, se acerca, sin llegar a tocarla nunca. Es una asíntota vertical. Una atracción permanente, un amor imposible. Foto de Petra, ciudad del año −312 excavada en la roca en la ladera del monte de Hor.

El milagro de las derivadas es que con cálculos numéricos podemos conocer la forma de una curva. Derivada positiva, curva creciente, derivada negativa, curva decreciente. Y si la derivada es cero el punto es de tangente horizontal, máximo relativo o mínimo o punto de inflexión, en ciertos casos.
En la foto un puente de Glen Coe, Highlands, Escocia que puede verse completa en el blog de viajes de Sabrina.

Estudiar una manzana con pimientos, porque éstos se conocen mejor, pero sin olvidar que es una manzana. Algo asi es un cambio de variable, muy útil en funciones, ecuaciones o integrales. Foto Ahmad Abusaad.
Esta entrada participa en la edición 4.123 del Carnaval de Matemáticas en el blog Eulerianos.

La naturaleza está llena de mates, con formas, cuerpos, figuras, curvas, simetrías, fractales, orden y regularidades. Pero no todo son mates y hoy nos hacemos eco del doodle homenaje a Maria Sibylla Merian, naturalista que con sus hermosos dibujos fue pionera de la entomología. Foto Heri Wijaya.
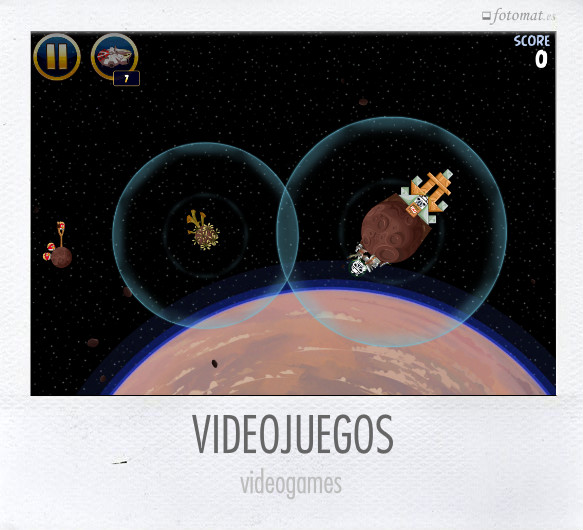
Los alumnos se quedan asombrados en clase de matemáticas cuando escuchan por primera vez que se usan muchas mates para desarrollar un videojuego. Luego van viendo que están llenos de mates: coordenadas, funciones, curvas, ecuaciones, intersecciones, vectores, condiciones, implicaciones… ¿cómo podrían realizarse sin mates?
Por ejemplo, BSVino presenta la serie Math for Game Developpers donde expone en videos el uso básico de vectores y fórmulas para mover personajes, hallar distancias o ralentizar movimientos.
En la foto una captura del juego Angry Birds.
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

Una mañana, exactamente al amanecer, un monje budista emprendió la ascensión de una elevada montaña. El sendero que utilizó, de no más de un metro de ancho, daba vueltas y revueltas en torno a la montaña, hasta un resplandeciente cerro en la cima. El monje fue subiendo con velocidad variable, deteniéndose muchas veces a descansar y a comer frutos secos que llevaba consigo. Alcanzó el templo poco antes de la puesta del sol. Tras varios días de ayuno y meditación, emprendió el viaje de regreso a lo largo del mismo sendero, partiendo al amanecer, caminando igualmente con velocidad variable y haciendo muchas pausas a lo largo del camino. Su velocidad media en el descenso fue, como era de esperar mayor que en el ascenso. Demostrar que hay un punto del camino por el que el monje pasó en ambos viajes exactamente a la misma hora del día.
Un problema clásico y que sorprende a primera vista. Esta versión del enunciado está tomada del club mensa, donde puede verse la solución clásica. Y hay otra más imaginativa.
Por cierto, buscando el problema del monje budista en google se entera uno de que más de la mitad de los monjes budistas son obesos. Ese debe ser su problema. Y es que a partir de las matemáticas se aprende de todo. Foto Petri Damstén.
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

Jean-Baptiste Joseph Fourier estudió hacia 1810 las que hoy llamamos en su honor series de Fourier, sumas infinitas que se recuerdan diciendo acósenos y bésenos. El matemático @LucasVB, especialista en visualizaciones interactivas de física y mates, nos presenta un Juego de Fourier, para manejar hasta 8 frecuencias, y su compañero @matthen2 demuestra de manera muy animada que toda función periódica es suma de series sinusoidales. Un gran resultado básico en el análisis armónico, con aplicaciones en ingeniería, matemática abstracta, análisis vibratorio, acústica, óptica, imágenes y señales, datos y telecomunicaciones. Un ejemplo de su uso se muestra en el esquemat de hoy. Foto Jumrus Leartcharoen.
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

El jugador más alto del mundo sería el máximo absoluto, el que se conforma con ser el más alto de su equipo, su barrio, su liga, es un máximo relativo. Y lo mismo con los mínimos. Apasionante cuestión la saber los puntos críticos de una función que se ve en la gráfica y se calcula haciendo nulas las derivadas. En la foto de 365díasdebasquet Manute, el jugador más alto de la historia de la NBA, con 2’31 m, y Tyrone, el más bajo, con 1’59 m.

El cielo está lleno de mates y hoy las nubes toman forma de dos curvas, las gráficas del seno y del coseno, que son iguales, aunque desplazadas. Dedicado a @encar77 que tuitea hermosas frases entra las que encontré esta foto, vía @tocamates.


