En tres capítulos, basados en rectángulos, círculos y triángulos, un precioso corto de animación:
Pure Geometry de Romanowsky.
Responder
Archivo de la etiqueta: figuras
Pentapájaro: Dícese de la figura formada por 5 pájaros. Del griego penta = cinco, como pentagrama, pentatlón, pentágono o Pentateuco. De los griegos nos vienen la geometría de Euclides y los descubrimientos de Thales, Pitágoras y tantos otros. Y del griego nos queda la nomenclatura, como polí(muchos)gonos(ángulos), tetra(cuatro)edro(caras), de ahí tetris, hipo(debajo)tenusa(alargar), homo(misma)morfismo(forma) o epi(sobre), endo(dentro), iso(igual) y auto(uno mismo). Y anti (contrario), hemi(mitad), micro(pequeño), mono(uno) y peri(alrededor de). Y usamos las ε, α, π, δ, Φ, Δ y, en Σuma, todo su αβeto. Foto Norbert Schipany.
Entrada para la Edición 4.12310 del Carnaval de Matemáticas en el blog de @_mirandamolina_.
Las matemáticas son un mundo en sí mismo. Y sirven para describir y prever fenómenos de todo tipo. Y también para modelar distintas realidades. El arquitecto y artista del papel australiano Horst Kiechle ha construido un torso geométrico de papel con el corazón, pulmones, intestinos, riñones, páncreas, estómago y todos los órganos. Cada pieza está diseñada por ordenador con triángulos y cuadriláteros numerados que se van montando y pegando hasta formar este auténtico cuerpo geométrico. Para no perderse las fotos de esta archisculpture ni la entrevista con el autor.
Entrada para la Edición 4.12310 del Carnaval de Matemáticas en el blog de @_mirandamolina_.
La Torre CN de Toronto ofrece a los turistas un aventurado paseo por los bordes de uno de los edificios más altos del mundo, 116 plantas = 356 metros = 1.168 pies. Un paseo perimetral para quien no le dé vértigo la geometría. Foto CNTower.
Muchas cosas tienen su origen en las matemáticas, otras pueden describirse con razonamientos y fórmulas matemáticas y otras más terminan pasando por las mates, como estos escarabajos, los míticos Beetles de Volkswagen, convertidos en cubos y esferas por el escultor Ichwan Noor en el Art Basel Hong Kong.
Dedicado a @GrupoDafy, @alef_mx, @TAB_ES, @Revista_Actual, @VeoArte, @CVida_arte y todos los que rompen las falsas barreras entre ciencia y arte.
Un cilindro se puede generar girando un rectángulo sobre uno de sus lados. Pero también podemos considerarlo como una columna de infinidad de círculos, según el principio de Cavalieri, precursor del cálculo integral para calcular volúmenes por secciones. Foto ulldefalcó.
Nos gustan las regularidades, las formas repetidas, los patrones, lo que se estudia en matemáticas como movimientos, transformaciones y teselaciones. Por la armonía de las formas, la lógica del desarrollo y la belleza del resultado son una práctica ideal para hacer con hijos y alumnos diseñando los patrones sobre un papel cuadriculado. Lo parasarán bien. Pero, eso sí, no les digas que son matemáticas.
Foto del post How to make a chevron pattern on stairs, donde explican e ilustran cómo hacer la plantilla y decorar una escalera.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.
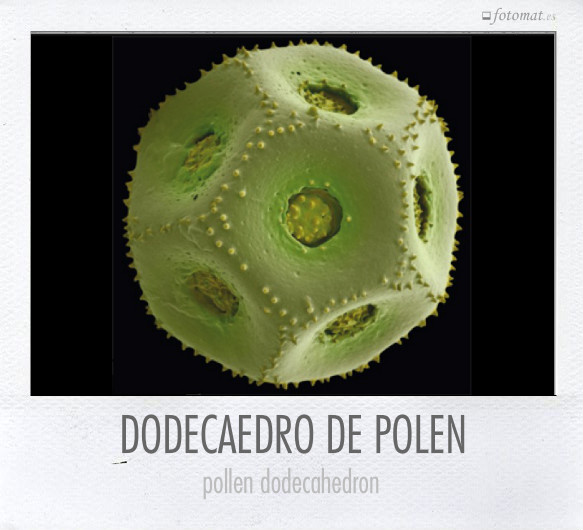
De lo más grande a lo más pequeño la naturaleza está llena de mates, a veces aún difíciles de describir y analizar, a veces en formas que requieren teorías avanzadas, como los espacios hiperbólicos o los fractales y a veces en formas básicas, como los cristales o este grano de polen seleccionado entre las magníficas fotografías microscópicas de Rob Kesseler. Su forma, un dodecaedro, 12 caras, pentágonos regulares. Cuando más conocemos más grande es el asombro ante la belleza, regularidad y optimización de todo lo que nos rodea.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.
Matemáticas que iluminan es conos truncados. Foto Artur Akobian.
La primera vez que vi el Teorema de Pick quedé sorprendido y un poco avergonzado de no conocerlo antes. Es un curioso y sorprendente resultado con el que se puede conocer el área de una región poligonal cuyos vértices están en una cuadrícula contando simplemente el nº de vértices y el de puntos de la cuadrícula que están dentro del polígono. Lo tiene todo para que los jóvenes estudiantes miren, prueben y vean las maravillas de las matemáticas. Habría que introducirlo en las clases de todas las edades, y a ello contribuyen la magnífica exposición de Mati y la demostración de gaussianos. ¡Ánimo!
En la foto de Eugene de Salignac pintores suspendidos en los cables del puente de Brooklyn en 1914.
Esta entrada participa en la edición 4.123 del Carnaval de Matemáticas en el blog Eulerianos.
