
Muchas funciones con expresiones sencillas en coordenadas polares producen gráficas llenas de simetrías, bucles y elegantes curvas. Pueden representarse en wolfram alpha escribiendo polar plot:
por ejemplo r=cos(7a/2), la espiral de Galileo r=10(1-3a2) o el escarabajo r=5cos(2a)-3cosa. Otra muestra son las flores polares realizadas con Desmos, la magnífica calculadora de gráficas on line de @Desmos. Foto Chalktrail, ingenioso juguete para pintar desde una bici financiado en kickstarter.
Resultados de la búsqueda para: funcion

Los vectores han pasado ya de las mats y la física a la vida cotidiana, están en las pantallas y en cualquier parte. Pero no se usan sólo para indicar direcciones, sino para llevar numerosos datos en varias dimensiones al mismo tiempo, como en los colores, videojuegos y todos los espacios vectoriales. Foto Mr dale, recogida por Alicia en su selección otoñal.

El recorrido de una función comprende todos los valores imagen de la misma. Algo así como si relacionando las fechas de un viaje con el destino juntamos las etiquetas de todos los lugares visitados. Eso sería el recorrido, imagen o rango de la función. Foto Kashif Izhar

Inventadas hacia 1960 por un ingeniero francés de la casa Renault, las curvas de Pierre Bézier han revolucionado el diseño introduciendo el dibujo vectorial en los ordenadores. Lo consiguen aproximando por trozos funciones polinómicas a cualquier curva por complicada que sea. Foto Thomas Lieser.

No sólo los violines llevan el símbolo integral. También lo encontramos en función de la escalera en esta hermosa foto de dickensian-dandy.

Entre las tendencias de las matemáticas destacan las de las sucesiones y funciones que pueden tender a un límite. Foto

Nuestra mirada, siempre simplificadora, busca acercar la realidad a líneas rectas y formas cuadradas. Y hay cosas que se ajustan a funciones de grado 2, como las formas cuadráticas, que describen cónicas y otras aplicaciones de un espacio vectorial en un cuerpo. Dedicado a todos los compañeros de las JAEM con esta foto de Anna Manrique en representación de las muchas y hermosas fotografías del concurso Vacaciones y Matemáticas que difunde @jaem2013. Enhorabuena a todos.
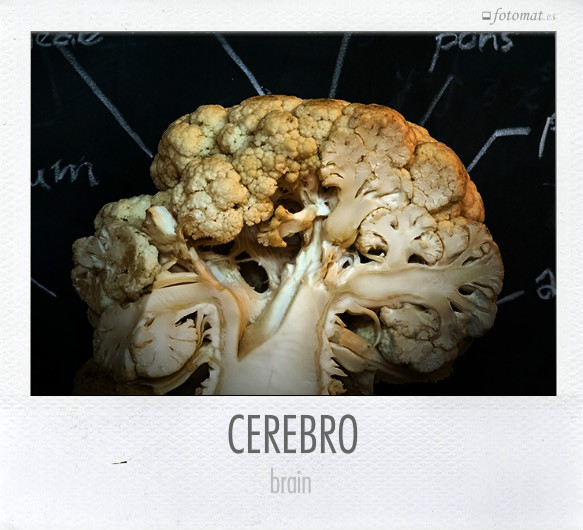
Las matemáticas siempre han sido reglas para la dirección de la mente, pero cada vez más proporcionan modelos para comprender y mejorar distintos funcionamientos del cerebro. Como la técnica anunciada hoy por el CSIC para visualizar la actividad de varios núcleos cerebrales interconectados por medio del análisis matemático, registros eléctricos y biofísica.
Foto de Paul van Geldrop que hace un modelo del cerebro a partir de la sección de una coliflor.

Una función es continua en un punto cuando un poco antes y un poco después se comporta sin saltos. Parece simple, pero ¿qué es un poco?¿y qué es un salto? Costó miles de años atreverse a formularlo y un par de siglos más formalizarlo. Es el cálculo infinitesimal, que permite razonar con cantidades infinitamente pequeñas. Foto continuidad de las olimpiadas entre London 2012 y Rio 2016

Si una parte de tu cuerpo está por encima del agua y otra parte por debajo, seguro que algo de tu cuerpo está exactamente en la superficie del agua. Siempre que el cuerpo sea continuo, claro. Es el Teorema de Bolzano, matemático checo cuya casa de Praga nos muestra @CamposdeTierra. Parece fácil y los conceptos que se entienden lo son, pero en el estudio de las funciones la cosa tiene su miga y es de gran utilidad. Foto David J. Phillip


