
Hoy se cumplen 25 años desde aquel 23 de junio de 1988 que vio el lanzamiento de SMP, el programa de cálculo simbólico, base de Mathematica, que desde entonces ha crecido en ideas y prestaciones y es la mejor herramienta de Matemáticas por computación y web, con una enorme potencia y utilidad en investigación, ingeniería, ciencia o farmacia y una gran vocación educativa.
Stephen Wolfram y su equipo celebran este 25 aniversario con un álbum de toda su historia y un recorrido de opiniones de usuarios. Lo celebramos aqui recomendando su portal MathWorld y su buscador de resultados Wolframalpha y presentando el Trébol de Moir y otras imágenes de arte matemático desarrollado con Mathematica .
Entrada para la Edición 4.12310 del Carnaval de Matemáticas en el blog de @_mirandamolina_.
Archivo de la categoría: estadística y probab.

Suceso imposible es el que no puede ocurrir, como encontrar un número negativo entre los naturales, meter una canasta en un partido de fútbol o sacar un 7 en un dado del 1 al 6. No hay ninguna probabilidad: P(∅)=0.
También es imposible tirar 12 dados y que queden como en la foto. Pero esa es otra historia.

Si una pelota flota sobre la cascada ¿cual es la probabilidad de que aparezca en cada una de las ramificaciones? Algo más sencilla es la máquina con la que el polímata, antropólogo, geógrafo, explorador, inventor, metereólogo, estadístico y psicólogo británico Francis Galton estudió probabilidades, dejando caer bolas por una tabla con clavos que iban separando caminos. Se utiliza para estudiar la distribución binomial y su relación con la distribución normal demostrando el teorema del límite central. Puede verse en acción la máquina de Galton, llamada también Quincunx, con el nombre de la moneda romana de 5 onzas, por la disposición de los clavos en forma del 5 de un dado o con el más castizo de Tresbolillo, como la disposición con que se siembran las plantas en triángulos equiláteros. Foto Lou Lu

La estatura de la población, la longitud de los granos de maíz, las notas de una clase y otras muchas cosas más se distribuyen de una forma que se llama normal. Hay pocos en los extremos y muchos en el centro, como ilustra la campana deGauss. La realidad nunca es exacta y perfecta, pero cuanto más casos se observen más se acerca a este modelo y se pueden predecir resultados con porcentajes y tablas de valores. Aunque lo normal es preferir verlo desde Santorini, isla griega de la foto.

Entre los gráficos estadísticos e infografícos más usados están el diagrama de barras, el de sectores llamado popularmente de quesitos, el pictograma y el polígono de frecuencias, como el de la foto donde Jim Van Raemdonck y el equipo de Phoebe De Corte crean infografías fisicamente a tamaño real para un Informe Anual. Hay histogramas, polígonos y quesitos, merece la pena ver el proceso.

No son pocas las relaciones de geometría con el arte, en cuanto a técnicas o diseños. La novedad ahora es un video juego de plataformas para la Play 3 donde nuestro héroe tiene que ir superando obstáculos inspirados en curvas e infografías.
Foto captura del vídeo promocional de Métrico de Digital Dreams.
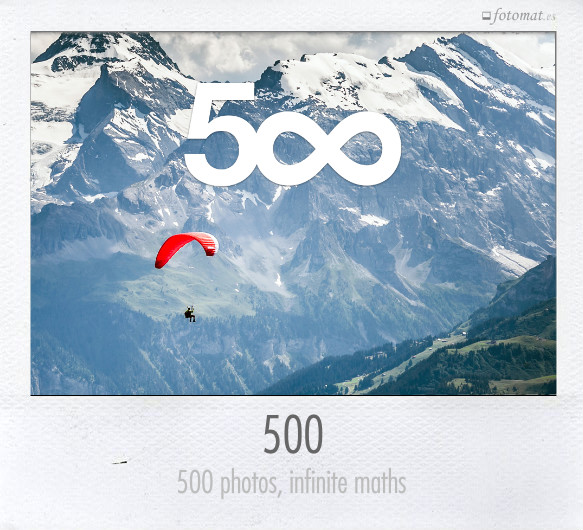
500 = quinientos = five hundred = D = 2²×5³ = 10²+20² = 4²+22² = 11110100₂ = 1f4₁₆
500 días, 500 fotos, ∞ matemáticas en fotomat.es, que celebramos con un homenaje a 500px.com, el gran portal de fotógrafos de alta calidad y gran variedad que lleva en su logo un infinito quinientos 5∞.
Gracias a todos los que cada día acompañáis y apoyáis este proyecto, que entre bromas y verás, sólo (¿sólo?) pretende alegrar, animar y aumentar, descubrir, desvelar y divulgar el conocimiento de las matemáticas, porque el mundo está lleno de mates.
La imagen es una captura en iPad de la portada de la extraordinaria App mobile de 500px, sobre una foto de SASIPA Muennuch.

¿De cuantas maneras pueden colocarse en línea 3 sillas azules, 3 rojas y una verde?
Son las permutaciones con repetición, una de las maneras de contar en teoría combinatoria.
Foto Emilio Cabida.

Fue Leonard Euler quien inició la teoría de grafos reduciendo el problema de los puentes de Könisgberg a una cuestión de puntos y líneas. Una idea tan simple (y tan genial) ha tenido un enorme desarrollo con aplicaciones en matemática discreta y computación, optimización, flujos y rutas. De todo ello da cuenta con claridad Mati en 4 artículos 4 sobre teoría de grafos, donde @ClaraGrima homenajea, además, al matemático mexicano Víctor Neumann-Lara. Foto Stanley Azzopardi.
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

Después de ver diagramas de barras, gráficos de sectores o de quesitos y pictogramas, entre los gráficos estadísticos, encontramos un polígono de frecuencias en esta foto de Julian Schulze.


