
Todo lo que no está en un conjunto está en su complementario. Si una cosa es A, la otra es no A. Sencillez y belleza de las matemáticas. Foto Krishan Bansal.
Archivos Mensuales: septiembre 2013

Si coloco a tal distancia de la pared una escalera de tales dimensiones ¿a qué altura llegaré?. Un típico problema de triángulos rectángulos que se lleva el sello de Pitágoras. Foto designsponge.

Diseño matemático, transparente, minimalista y funcional de un lavabo paralelepípedo regular. Foto worclip.

Se pueden construir muchas circunferencias que pasan por 2 puntos y solo una que pasa por 3 puntos dados. Y otras que pasan por los centros de 3 circunferencias o que son tangentes a rectas o curvas y otros muchos y apasionantes problemas clásicos de construcciones geométricas que a lo largo de la historia han unido pasión, lógica y experiencia estética. Foto Murat İbranoğlu.

Tenemos aquí un verdadero puente tangente, formado por las tangentes a la curva inferior del puente. Es lo que se llama la curva envolvente a una familia de, en este caso, rectas, como podemos ver en el esquemat de hoy. Foto puente matemático de Cambrige. La disposición de las maderas le da una estructura rígida y autoportante muy eficiente. Las vigas radiales soportan sobre todo fuerzas de compresión, con muy poco esfuerzo de flexión.
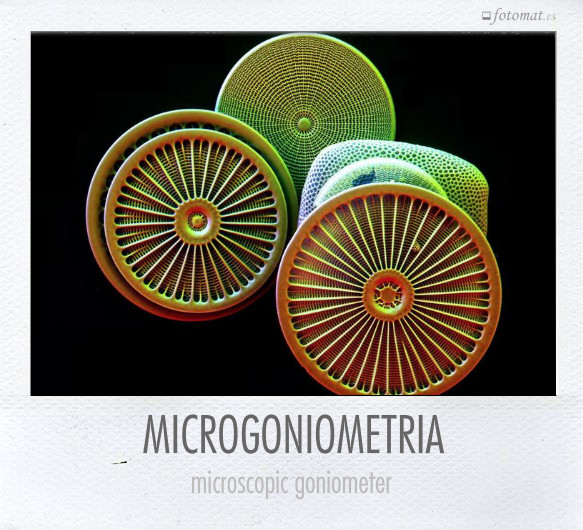
En palabras de Galileo ❝El Universo está escrito en el lenguaje de las matemáticas❞. En lo grande y en lo pequeño encontramos las mismas formas y relaciones sencillas. La circunferencia goniométrica y las coordenadas polares aparecen en esta imagen tomada con el EVO scanning electron.

Vayes donde vayes encontrarás matemáticas. Y a veces a lo grande, como esta fórmula del teorema de Bayes para la probabilidad condicional, diseñado en azules luces de neón, que se encuentra en Cambridge.

Un concepto sencillo, pero básico, el vértice de una figura plana en una magnífica foto de Łukasz Jabłoński.

Si marcamos en coordenadas cartesianas los valores que toma un polinomio tenemos una gráfica continua que puede tener más máximos y mínimos cuanto mayor sea su grado, como se ve en el análisis de grados de esquemat. Como la silueta de la foto de Jacques-André Dupont que, con 8 máximos, 7 mínimos y 14 puntos de inflexión, debería ser, al menos de grado 16.

A veces las cosas parecen compactas, pero mirándolas de otra manera se descubren sus partes. Como se pueden factorizar los números en factores primos y los polinomios en primarios. Y como las fotos en color, que se descomponen en factores. Y como esta Bicycle Art in Street que sería
bici = ❍² Λ Δ ∇


