
Una circunferencia puede estar respecto a otra en posición exterior, tangente o interior como nos muestran (casi) estas llantas de rueda de carro de la hermosa foto de Pam Jones. Aunque también podrían cortarse en dos puntos, ser tangentes interiores y concéntricas.
Archivos Mensuales: mayo 2013

La cinta de Moebius causa asombro y fascinación porque muestra claramente una figura en el espacio que tiene una sola cara. Y no sólo en geometría sino también en el arte como muestra la foto de esta escultura del diseñador Max Bill.

Si una pelota flota sobre la cascada ¿cual es la probabilidad de que aparezca en cada una de las ramificaciones? Algo más sencilla es la máquina con la que el polímata, antropólogo, geógrafo, explorador, inventor, metereólogo, estadístico y psicólogo británico Francis Galton estudió probabilidades, dejando caer bolas por una tabla con clavos que iban separando caminos. Se utiliza para estudiar la distribución binomial y su relación con la distribución normal demostrando el teorema del límite central. Puede verse en acción la máquina de Galton, llamada también Quincunx, con el nombre de la moneda romana de 5 onzas, por la disposición de los clavos en forma del 5 de un dado o con el más castizo de Tresbolillo, como la disposición con que se siembran las plantas en triángulos equiláteros. Foto Lou Lu

Periódico es lo que se repite regularmente, como los números periódicos y funciones periódicas. Y también los diarios o periódicos, que siguen un proceso de redacción-decisión-confección-impresión-distribución que se repite en intervalos regulares cada día. Y las revistas semanales o mensuales, con períodos de 7 y 30 días. Y el Carnaval de Matemáticas, que se repite cada mes. Y el fotomat y el esquemat, de período 24 horas. Foto Maynard Owen, seleccionada en los 125 años de National Geographic.

Descansando un poco de los puros conceptos nos adentramos hoy en la magia de las matemáticas, la fascinación por comprender el cosmos que llevó a Galileo, Kepler, Newton y tantos otros a acercarse más y más al conocimiento de las leyes que rigen el universo. Contemplando esta magnífica foto de la luna enviada por @licmonicag, profesora de mates y tecnología. Gracias.

De tipos = letras de imprenta y metría = medida, la tipometría es el sistema de medición de tipografía. En base 12, la unidad es el punto y su múltiplo el cícero o pica = 12 pt. Pero hay distintos sistemas de puntos: en casi todo el mundo se impuso el iniciado por Fournier (1737) y perfeccionado por Didot (1760) en el que 1 punto = 1/(12x12x12) pie de rey = 0’376 mm y 1 cícero = 12 pt = 4’512 mm. Para las imprentas de Inglaterra y Estados Unidos se aprobó en 1860 un sistema basado en la pulgada inglesa con 1 pt = 1/72 “= 0’352 mm y 1 pica = 12 pt = 4’24 mm. Es el sistema anglosajón, que se ha impuesto como punto postscrip para la autoedición en ordenadores. Y todo ello medido con el tipómetro, la regla graduada para trabajar con medidas tan pequeñas. Un mundo “impresionante” que se desvela en el magnífico blog unostiposduros. Foto de la tipoteca de Lola Espinosa.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Nos gustan las regularidades, las formas repetidas, los patrones, lo que se estudia en matemáticas como movimientos, transformaciones y teselaciones. Por la armonía de las formas, la lógica del desarrollo y la belleza del resultado son una práctica ideal para hacer con hijos y alumnos diseñando los patrones sobre un papel cuadriculado. Lo parasarán bien. Pero, eso sí, no les digas que son matemáticas.
Foto del post How to make a chevron pattern on stairs, donde explican e ilustran cómo hacer la plantilla y decorar una escalera.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.
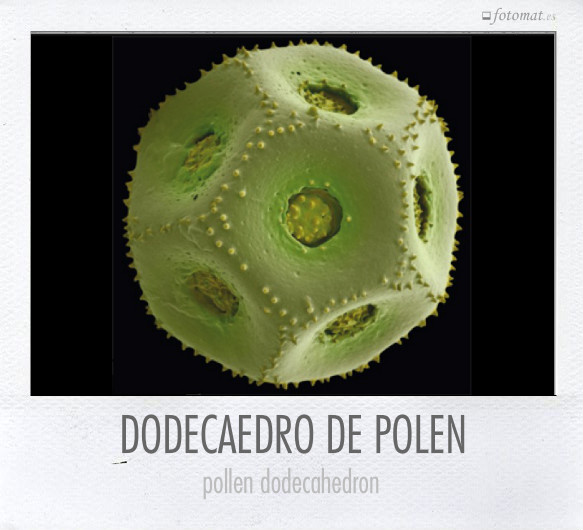
De lo más grande a lo más pequeño la naturaleza está llena de mates, a veces aún difíciles de describir y analizar, a veces en formas que requieren teorías avanzadas, como los espacios hiperbólicos o los fractales y a veces en formas básicas, como los cristales o este grano de polen seleccionado entre las magníficas fotografías microscópicas de Rob Kesseler. Su forma, un dodecaedro, 12 caras, pentágonos regulares. Cuando más conocemos más grande es el asombro ante la belleza, regularidad y optimización de todo lo que nos rodea.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

El concepto de velocidad media es sencillo, basta dividir lo que andas entre lo que tardas, pero para afinar más y trabajar con velocidad instantánea hubo que inventar las derivadas y todo el cálculo infinitesimal de Newton y Leibnitz, con sus épsilons, infinitésimos, límites y funciones continuas, basado todo en los números reales, indispensables para ello. Foto National Geographic.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

1 cuerno de 2, la mitad de los cuernos, 1/2, ¿tiene medio cuerno? No, tiene la mitad de los cuernos, en decimales 0’5 del total de cuernos que debía. Son números racionales, de razón = a/b (de donde vienen las proporciones), fracciones y decimales que sirven para conocer y calcular con partes no enteras de las cosas. Foto Kellie Reifstenzel para el National Geographic Traveler Photo Contest.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.


